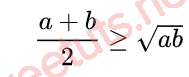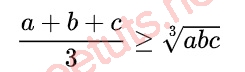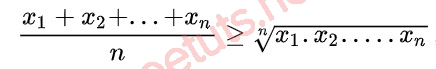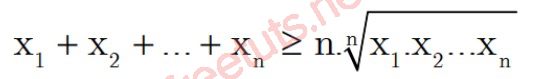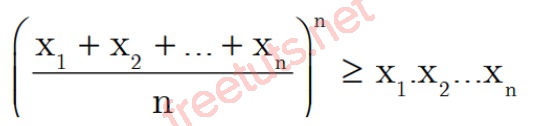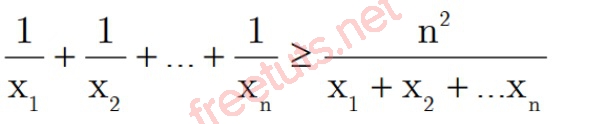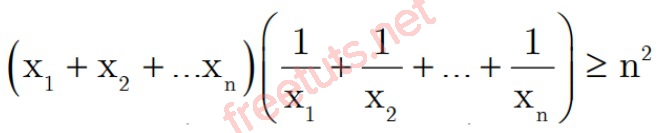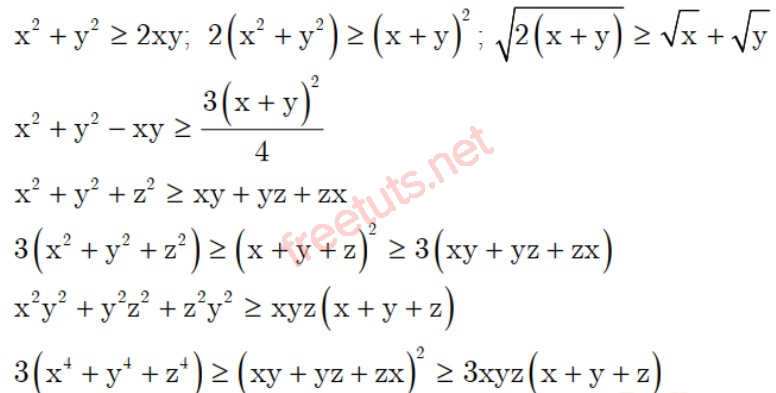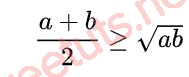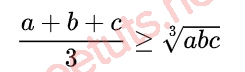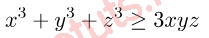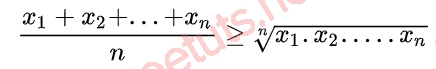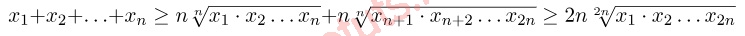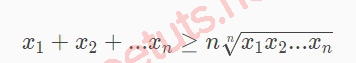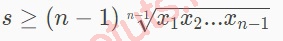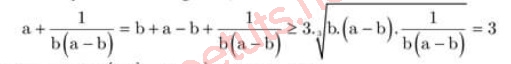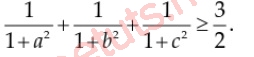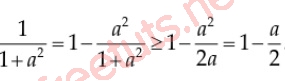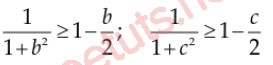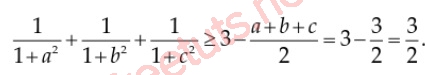Bất đẳng thức Cosi hoặc thường hay gọi là bất đẳng thức AM - GM là BĐT được dùng để làm đối chiếu thân thuộc tầm nằm trong và tầm nhân của những số thực ko âm.

Bạn đang xem: Bất đẳng thức Cosi: Công thức, hệ quả và các bài tập

Bài viết lách này được đăng bên trên dattruoc-yamahaneos.vn, ko được copy bên dưới từng mẫu mã.
Bất đẳng thức Cosi là 1 trong kiến thức và kỹ năng toán học tập vô nằm trong cần thiết nhập công tác trung học cơ sở, đó là nền móng hùn những em học viên lớp 8 và 9 giải những Việc tương quan cho tới phương trình và bất phương trình hiệu suất cao nhất. Chính chính vì thế, nhập nội dung bài viết ngày hôm nay, hãy nằm trong freetuts ôn tập dượt lại những kiến thức và kỹ năng tương quan cho tới bất đẳng thức Cauchy và những dạng bài xích tập dượt tương quan nha.
Tìm hiểu về bất đẳng thức Cosi
Định nghĩa bất đẳng thức Cosi
Trong toán học tập, bất đẳng thức Cô si là bất đẳng thức được dùng để làm đối chiếu thân thuộc tầm nằm trong và tầm nhân của những số thực ko âm.
Ai là kẻ sáng tạo rời khỏi bất đẳng thức Cosi?
Tên đích thị của bất đẳng thức này là hoặc mang tên không giống là bất đẳng thức AM - GM, nhập đó: AM là viết lách tắt của Arithmetic mean, GM là viết lách tắt của Geometric mean. Và BĐT này còn có rất rất rất nhiều cách thức minh chứng tuy nhiên mái ấm toán học tập người Pháp là Augustin – Louis Cauchy (Cosi, Theo phong cách phát âm giờ đồng hồ Việt) đã mang rời khỏi cơ hội minh chứng quy hấp thụ dễ dàng nắm bắt nhất nên nhiều người đang được lầm lẫn rằng BĐT AM - GM là vì ông sáng tạo rời khỏi.
Bài viết lách này được đăng bên trên [free tuts .net]
Bất đẳng thức Cô si được dùng để làm thực hiện gì?
Bất đẳng thức Cauchy là 1 trong trong mỗi kiến thức và kỹ năng vô nằm trong cần thiết và thông dụng nhập công tác toán trung học cơ sở, nó được dùng nhằm giải những dạng toán tương quan cho tới phương trình, bất phương trình và thám thính độ quý hiếm lớn số 1 hoặc bé nhỏ nhất của biểu thức.
Các dạng bất đẳng thức Cosi nhập toán học
Bất đẳng thức AM - GM (Cosi) rất có thể được tuyên bố bên dưới những dạng sau:
Dạng 1: Dạng tổng quát tháo bđt Cosi
Trung bình nằm trong của n số thực ko âm tiếp tục luôn luôn trực tiếp to hơn hoặc vì chưng tầm nhân của những số thực này, và tầm nằm trong chỉ vì chưng tầm nhân khi n số thực này cân nhau.
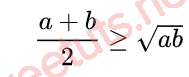
Dấu “=” xẩy ra khi a = b.
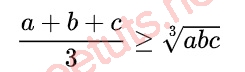
Dấu “=” xẩy ra khi a = b = c.
-
Bất đẳng thức Cosi không ngừng mở rộng với x1, x2,...xn, n là số thực ko âm, tao có:
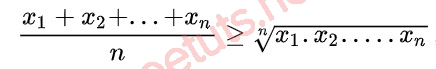
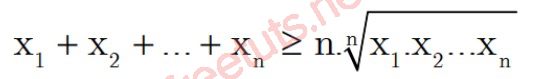
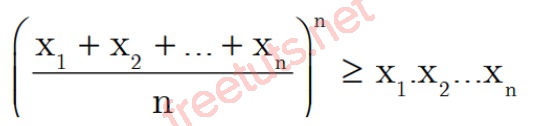
Dấu “=” xẩy ra khi x1 = x2 =...xn.
Với x1, x2,...xn, n là số thực dương, tao có:
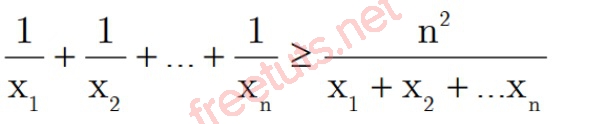
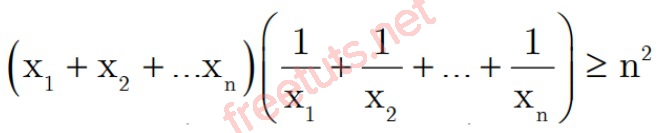
Dấu “=” xẩy ra khi x1 = x2 =...xn.
Dạng 2: Các tình huống đặc trưng của bất đẳng thức Cauchy
Trong tình huống n = 2 và n = 3, tao đem một trong những dạng trình diễn đặc trưng như sau:
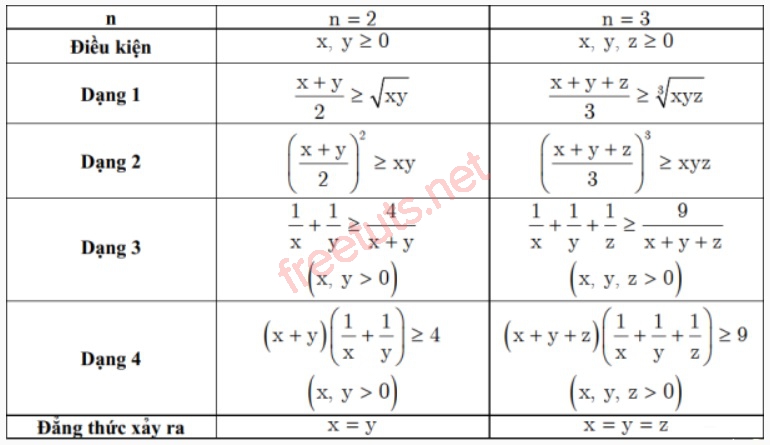
Dạng 3: Một số bất đẳng thức được suy rời khỏi kể từ bđt Cauchy
Từ bất đẳng thức Cô si, tất cả chúng ta rất có thể suy rời khỏi một trong những bất đẳng thức khác ví như sau:
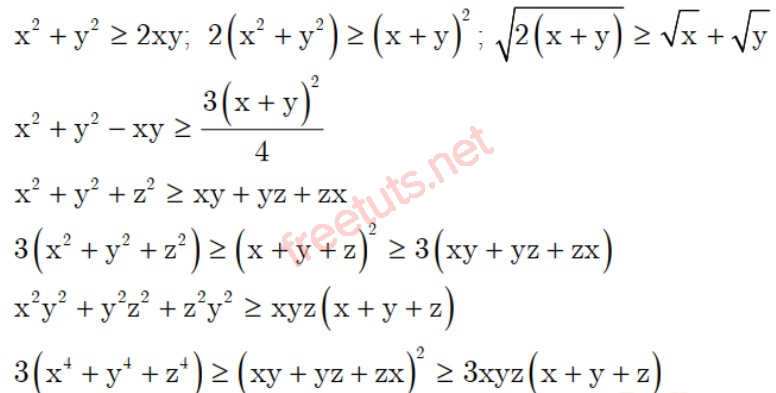
Hệ trái khoáy bất đẳng thức Cosi lớp 9
Từ bất đẳng thức Cauchy, tất cả chúng ta đem một trong những hệ trái khoáy sau:
a + 1/a ≥ 2, ∀ a > 0
- Hệ trái khoáy 2: Cho nhị số thực dương ngẫu nhiên (a, b), nếu như tổng (a+b) ko thay đổi thì tích của (a.b) có mức giá trị rộng lớn nhất lúc a = b.
- Hệ trái khoáy 3: Cho nhị số thực dương ngẫu nhiên, nếu như tích của chính nó ko thay đổi thì tổng của 2 số này còn có độ quý hiếm nhỏ nhất lúc 2 số này cân nhau.
Cách minh chứng bất đẳng thức Cauchy
Có rất rất rất nhiều cách thức minh chứng bất đẳng thức Cauchy, những em hãy nằm trong xem thêm một trong những những cách thức minh chứng bất đẳng thức này tức thì tiếp sau đây nha:
Chứng minh bất đẳng thức Cosi mang lại 2 số dương
Cho a, b ∈ R; minh chứng rằng:
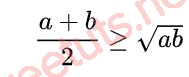
⇔ a + b ≥ 2 căn bậc 2 của (a x b)
⇔ a - 2 căn bậc 2 của (a x b) + b ≥ 0
⇔ (căn a - căn b)^2 ≥ 0 (luôn đích thị với từng a, b ≥ 0)
Như vậy, tao đang được minh chứng được BĐT cauchy luôn luôn đích thị với 2 số thực dương.
Chứng minh bất đẳng thức cosi mang lại 3 số thực ko âm
Với a, b, c là số thực dương, hãy minh chứng BĐT sau:
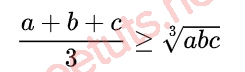
Ta có:
Đặt x = căn bậc 3 của a, hắn = căn bậc 3 của b, z = căn bậc 3 của c, nên tao đem x, hắn, z ≥ 0,
⇒ x + hắn + z ≥ 0.
Lúc này, bất đẳng thức quy về dạng
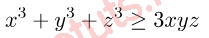

Vậy tao đem vấn đề cần minh chứng, và vệt “=” xẩy ra khi và chỉ khi x = hắn = z, hoặc tương tự a = b = c.
Chứng minh BĐT Cosi với n số thực ko âm
Với x1, x2,...xn, n là số thực ko âm, hãy minh chứng BĐT sau là đích thị.
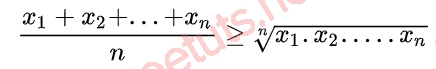
Ta đang được minh chứng được BĐT Cosi luôn luôn đích thị với 2 số thực dương, suy rời khỏi n = 2 thì BDT Cosi bên trên luôn luôn đích thị.
Để minh chứng BĐT bên trên đích thị với n số thì tất cả chúng ta rất có thể minh chứng nó cũng giống với 2n số.
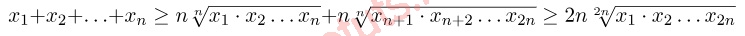
Áp dụng đặc thù quy hấp thụ, tao đem bất đẳng thức bên trên tiếp tục luôn luôn đích thị với n là 1 trong lũy quá của 2.
Gỉa sử BĐT Cosi luôn luôn đích thị với n số, tao cũng tiếp tục minh chứng được nó luôn luôn đích thị với n - một số ít như sau:
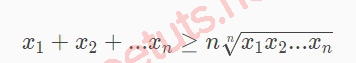
Gọi xn = S/(n - 1), với S = x1 + x2 +...+ xn
Suy ra:
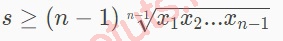
Như vậy, tao đem, BĐT Cosi luôn luôn đích thị với 2n và (n - 1) số, vậy, tao rất có thể suy rời khỏi bất đẳng thức Cauchy tiếp tục đích thị với n số thực ko âm.
Lưu ý khi dùng bất đẳng thức AM - GM (Cosi)
Khi dùng bất đẳng thức Cauchy, chúng ta cần thiết cảnh báo một trong những điều sau:
Xem thêm: Đề về 80 hôm sau đánh con gì - Đề về 80 mai đánh lô gì
- Bất đẳng thức Co si chỉ đích thị với những số thực ko âm.
- Chỉ nên vận dụng bất đẳng thức Cô si khi BĐT cần thiết minh chứng đem tổng và tích.
- Luôn ghi nhớ, vệt “=” chỉ xẩy ra khi những số cân nhau.
Dạng bài xích tập dượt về bất đẳng thức Cosi
Như vậy, những em đang được bắt được những kiến thức và kỹ năng tương quan cho tới BĐT Cosi rồi đúng không ạ này, giờ đây hãy vận dụng bọn chúng nhằm lên đường giải một trong những dạng bài xích tập dượt tuy nhiên freetuts đang được liệt kê tức thì tiếp sau đây nha:
Dạng 1: kề dụng thẳng BĐT Côsi nhập bài xích tập dượt minh chứng bất đẳng thức
Ví dụ: Cho 2 số dương a, b thỏa mãn nhu cầu a^2 + b^2 = 2, hãy bệnh minh:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4
Lời giải:
Vì a, b > 0 nên suy rời khỏi a/b > 0, b/a > 0, a/b^2 > 0, b/a^2 >0.
Áp dụng bdt Cosi, tao có:
a/b + b/a ≥2 căn bậc nhị (a/b x b/a) = 2
a/b^2 + b/a^2 ≥2 căn bậc nhị (a/b^2 + b/a^2 ) = 2/(căn bậc 2(a x b)
Suy ra:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4/(căn bậc 2 của a x b) (1)
Mà tao có:
2 = a^2 + b^2 ≥ 2 x (căn bậc 2 của a^2 x b^2) = 2.a.b
⇒ a.b ≤ 1 (2)
Kết ăn ý (1) và (2), tao có:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4 (điều nên bệnh minh),
Dấu “=” xẩy ra khi a = b = 1.
Dạng 2: Kỹ thuật thêm thắt bớt nhập bất đẳng thức Côsi
Đối với dạng toán này, những em hãy chuyển đổi BĐT rất cần được bệnh bản thân bằng phương pháp nhân, phân chia hoặc thêm thắt bớt một trong những, nhằm rất có thể giản dị và đơn giản được BĐT lúc đầu.
Lưu ý: Khi tách và vận dụng BDT cosi, nên nhờ vào việc đáp ứng mang lại vệt “=” xẩy ra.
Ví dụ: Cho a, b là số thực dương, sao mang lại a > b, minh chứng rằng:
a + 1/(b.(a - b) ≥ 3.
Lời giải:
Coi 1/(b.(a - b), b, (a - b) là 3 số dương, ap dụng bất đẳng thức Co si mang lại 3 số dương tao có:
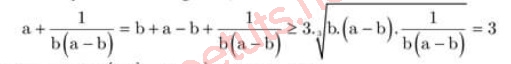
Dấu vì chưng xẩy ra, khi và chỉ khi:
a - b = b = 1/(b.(a - b) ⇔ a = 2; b = 1.
Dạng 3: Tìm độ quý hiếm lớn số 1, bé nhỏ nhất của biểu thức
Ví dụ: Bài tập dượt thám thính GTLN, GTNN vì chưng bất đẳng thức Cosi lớp 9
Cho nhị số dương a, b. Tìm độ quý hiếm lớn số 1 (GTLN) hoặc độ quý hiếm nhỏ nhất (GTNN) của những biểu thức nhập tình huống sau:
a. a + b = 8, thám thính GTLN của A = (a + b ).a.b
b. a.b = 6 ko thay đổi, thám thính GTNN của biểu thức B = (a + b)/ (a^2.b^2)
Lời giải:
Vì a + b = 8 nên tao đem A = (a + b ).a.b = 8ab.
Áp dụng hệ trái khoáy bất đẳng thức cô si, tao có:
A đạt GTLN khi và chỉ khi (a x b) max ⇔ a = b (1)
Ta có: a + b = 8, a = b ⇒ a = b = 4.
Vậy A max = 6.4.4 = 96.
Vậy A đạt độ quý hiếm lớn số 1 là 96 khi a = b = 4.
b. Ta đem B = (a + b)/ (a^2.b^2) = (a + b)/9^2 = (a + b)/81 vì như thế a.b = 9 luôn luôn ko thay đổi.
Áp dụng hệ trái khoáy BĐT cosi, tao có:
B min ⇔ (a + b) min ⇔ a = b.
Lúc này tao có: a = b; a.b = 9 ⇒ a = b = 3.
Vậy B min = (3 + 3)/81 = 2/27
Vậy độ quý hiếm nhỏ nhất của B là 2/27 khi a = 3 = 3.
Dạng 4: Ứng dụng BDT Cosi ngược vệt nhằm minh chứng bất đẳng thức
Ví dụ minh họa bài xích tập dượt về bất đẳng thức Cosi lớp 9
Cho 3 số thực a, b , c ko âm, to hơn 0 và a + b + c = 3, minh chứng rằng:
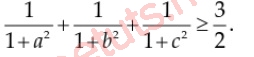
Lời giải:
Vì a + b + c = 3; a, b, c >0, nên tao thấy điểm rơi của bpt bên trên a = b = c = 1.
Áp dụng bđt Cosi mang lại kiểu mẫu số, tao có:
a^2 + 1 ≥ 2a ⇔ 1/(1+a^2) ≤ 1/2a
Ta thấy, thời điểm hiện tại vệt của bdt tiếp tục trái hướng đối với đòi hỏi của đề bài xích.
Lúc này, vận dụng Cosi ngược vệt, tao có:
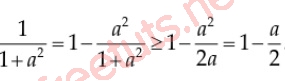
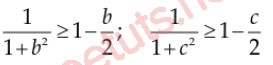
Cộng vế bám theo vế, tao có:
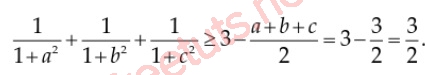
Vậy tao đang được đem điều nên minh chứng.
Hỏi đáp về BDT Cosi
Bất đẳng thức Cosi học tập ở lớp mấy?
Các em sẽ tiến hành học tập kiến thức và kỹ năng về BĐT Cosi nhập công tác toán lớp 9 nha.
Xem thêm: Giấy chứng nhận vệ sinh an toàn thực phẩm
Bất đẳng thức Cauchy-Schwarz liệu có phải là tên thường gọi không giống của BĐT Cosi không?
Các em chớ lầm lẫn thân thuộc điều này nha, nhị BĐT này trọn vẹn không giống nhau bại liệt, BĐT Cauchy-Schwarz hoặc thường hay gọi là bất đẳng thức Bunhiacopxki là BĐT bởi 3 mái ấm toán học tập Augustin Louis Cauchy, Viktor Yakovlevich Bunyakovsky và Hermann Amandus Schwarz sáng tạo rời khỏi.
Như vậy, qua chuyện nội dung bài viết bên trên, dattruoc-yamahaneos.vn đang được share những kiến thức và kỹ năng tương quan về bất đẳng thức Cosi, những công thức, cơ hội minh chứng và một trong những dạng bài xích tập dượt tương quan. Hy vọng nội dung bài viết nãy sẽ hỗ trợ những em ôn luyện và nắm rõ được kiến thức và kỹ năng cần thiết này. Chào từ biệt và hứa tái ngộ những em trong những bài xích đăng tiếp theo sau nhằm cùng với nhau thám thính hiểu thêm thắt nhiều kiến thức và kỹ năng toán học tập thú vị không giống nha!